Pearson's Correlation Coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the linear correlation between two variables X and Y, giving a value between +1 and −1 inclusive, where 1 is total positive correlation, 0 is no correlation, and −1 is total negative correlation. It is widely used in the sciences as a measure of the degree of linear dependence between two variables.
Pearson's correlation coefficient is the covariance of the two variables divided by the product of their standard deviations.
Pearson's correlation coefficient when applied to a population is commonly represented by the Greek letter ρ (rho) and may be referred to as the population correlation coefficient or the population Pearson correlation coefficient. The formula for ρ[7] is:
-
- where:
is the covariance
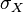is the standard deviation of 
- where:
The formula for ρ can be expressed in terms of mean and expectation. Since
![\operatorname{cov}(X,Y) = \operatorname{E}[(X-\mu_X)(Y-\mu_Y)]](https://upload.wikimedia.org/math/8/5/e/85eb69fa2d810acdd879236a624c927d.png)
Then the formula for ρ can also be written as
![\rho_{X,Y}=\frac{\operatorname{E}[(X-\mu_X)(Y-\mu_Y)]}{\sigma_X\sigma_Y}](https://upload.wikimedia.org/math/e/0/1/e0150d5feea4091277abdcbd9db35fc9.png)
-
- where:
- and 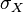are defined as above
is the mean of 
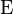is the expectation.
- where:
The formula for ρ can be expressed in terms of uncentered moments. Since
![\mu_X=\operatorname{E}[X]](https://upload.wikimedia.org/math/2/1/3/213ddf84ba1cc6977c32c55298633f79.png)
![\mu_Y=\operatorname{E}[Y]](https://upload.wikimedia.org/math/5/0/7/507f97ca0759fff54ce4de46a70b4301.png)
![\sigma_X^2=\operatorname{E}[(X-\operatorname{E}[X])^2]=\operatorname{E}[X^2]-\operatorname{E}[X]^2](https://upload.wikimedia.org/math/9/1/4/9146607a529c5827a45c1ec27005f85e.png)
![\sigma_Y^2=\operatorname{E}[(Y-\operatorname{E}[Y])^2]=\operatorname{E}[Y^2]-\operatorname{E}[Y]^2](https://upload.wikimedia.org/math/5/7/d/57db9bf0e1ab9915656ae72f890e8017.png)
![\operatorname{E}[(X-\mu_X)(Y-\mu_Y)]=\operatorname{E}[(X-\operatorname{E}[X])(Y-\operatorname{E}[Y])]=\operatorname{E}[XY]-\operatorname{E}[X]\operatorname{E}[Y],\,](https://upload.wikimedia.org/math/4/3/3/433542b21e76326cc35511b216b2b6e7.png)
Then the formula for ρ can also be written as
![\rho_{X,Y}=\frac{\operatorname{E}[XY]-\operatorname{E}[X]\operatorname{E}[Y]}{\sqrt{\operatorname{E}[X^2]-\operatorname{E}[X]^2}~\sqrt{\operatorname{E}[Y^2]- \operatorname{E}[Y]^2}}.](https://upload.wikimedia.org/math/3/a/8/3a8fd48ed9d34d02cb87f2604dc50c50.png)
- Covariance is a measure of how much two random variables change together. If the greater values of one variable mainly correspond with the greater values of the other variable, and the same holds for the smaller values, i.e., the variables tend to show similar behavior, the covariance is positive.[1] In the opposite case, when the greater values of one variable mainly correspond to the smaller values of the other, i.e., the variables tend to show opposite behavior, the covariance is negative. The sign of the covariance therefore shows the tendency in the linear relationship between the variables. The magnitude of the covariance is not easy to interpret. The normalized version of the covariance, the correlation coefficient, however, shows by its magnitude the strength of the linear relation.
- Correlation is a technique for investigating the relationship between two quantitative, continuous variables, for example, age and blood pressure. Pearson's correlation coefficient (r) is a measure of the strength of the association between the two variables.The first step in studying the relationship between two continuous variables is to draw a scatter plot of the variables to check for linearity. The correlation coefficient should not be calculated if the relationship is not linear. For correlation only purposes, it does not really matter on which axis the variables are plotted. However, conventionally, the independent (or explanatory) variable is plotted on the x-axis (horizontally) and the dependent (or response) variable is plotted on the y-axis (vertically).The nearer the scatter of points is to a straight line, the higher the strength of association between the variables. Also, it does not matter what measurement units are used.
Values of Pearson's correlation coefficient
Pearson's correlation coefficient (r) for continuous (interval level) data ranges from -1 to +1:r = -1 data lie on a perfect straight line with a negative slope r = 0 no linear relationship between the variables r = +1 data lie on a perfect straight line with a positive slope Positive correlation indicates that both variables increase or decrease together, whereas negative correlation indicates that as one variable increases, so the other decreases, and vice versa.
No comments:
Post a Comment